在高精度方面，专注于发展基于高阶数值格式如通量重构方法的气动声学计算工具。具体来说，通过数值求解时域的声学控制方程如波动方程、线化欧拉方程和欧拉方程等，得到高精度的声场信息，进而系统分析流动与声波的相互耦合问题。当前构造了一种能量稳定的通量重构格式来避免计算中产生数值耗散和色散，并基于一维线化欧拉方程进行了详细的验证和分析。

  对于高频的大尺度声传播问题，高效率的求解成为了主要的需求。通过发展适用于具有流动的复杂环境的高斯波束追踪方法，从几何声学的角度高效地求解大尺度的声传播问题，为环境噪声治理、海洋噪声分析等实际问题提供支撑。

  当前提出了改进的高斯波束追踪方法来计算流动中声传播的问题，并对二维涡对点声源的声场的影响进行了详细的计算和分析。

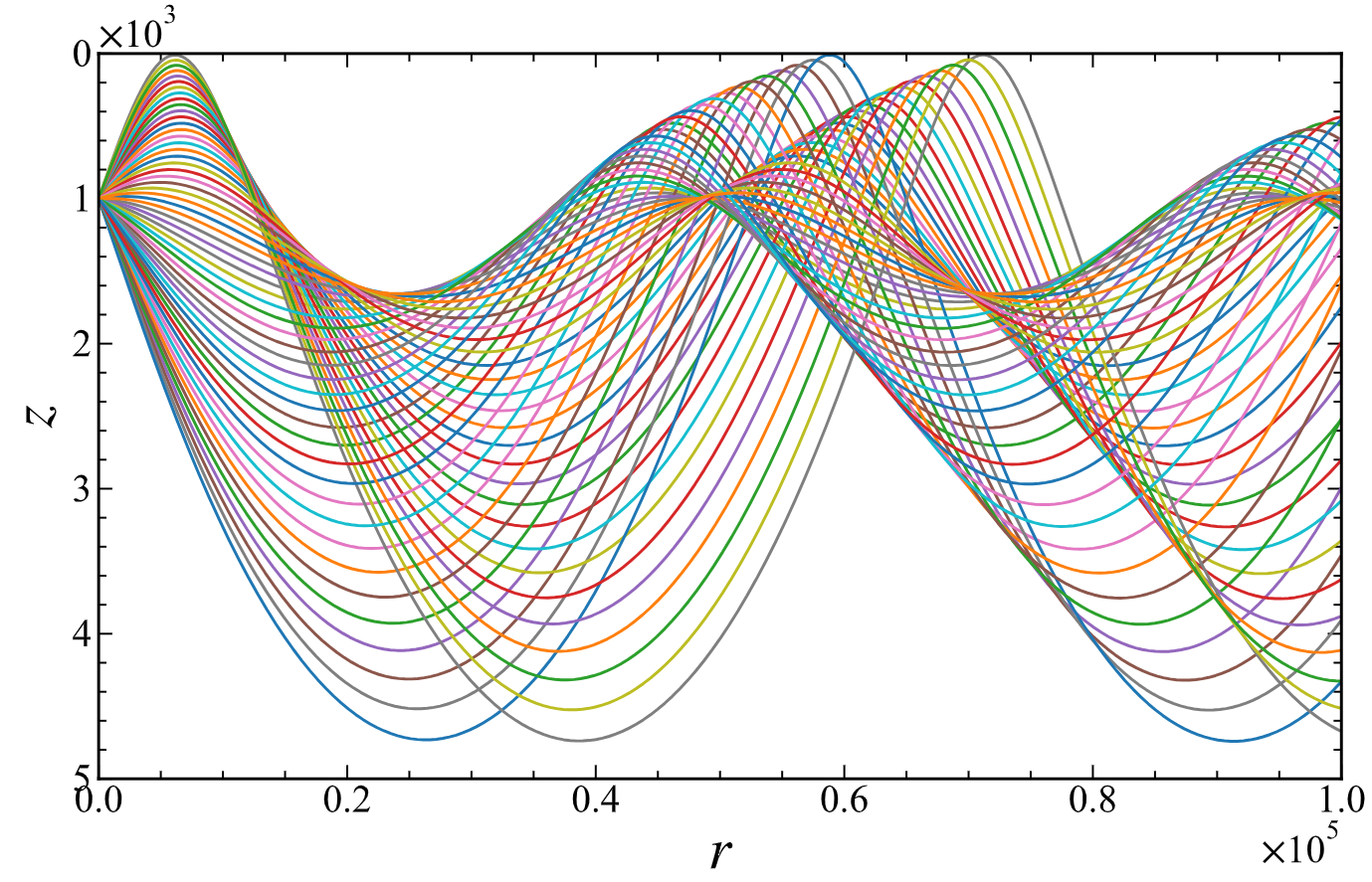
图 1 海底声线轨迹（几何声学）

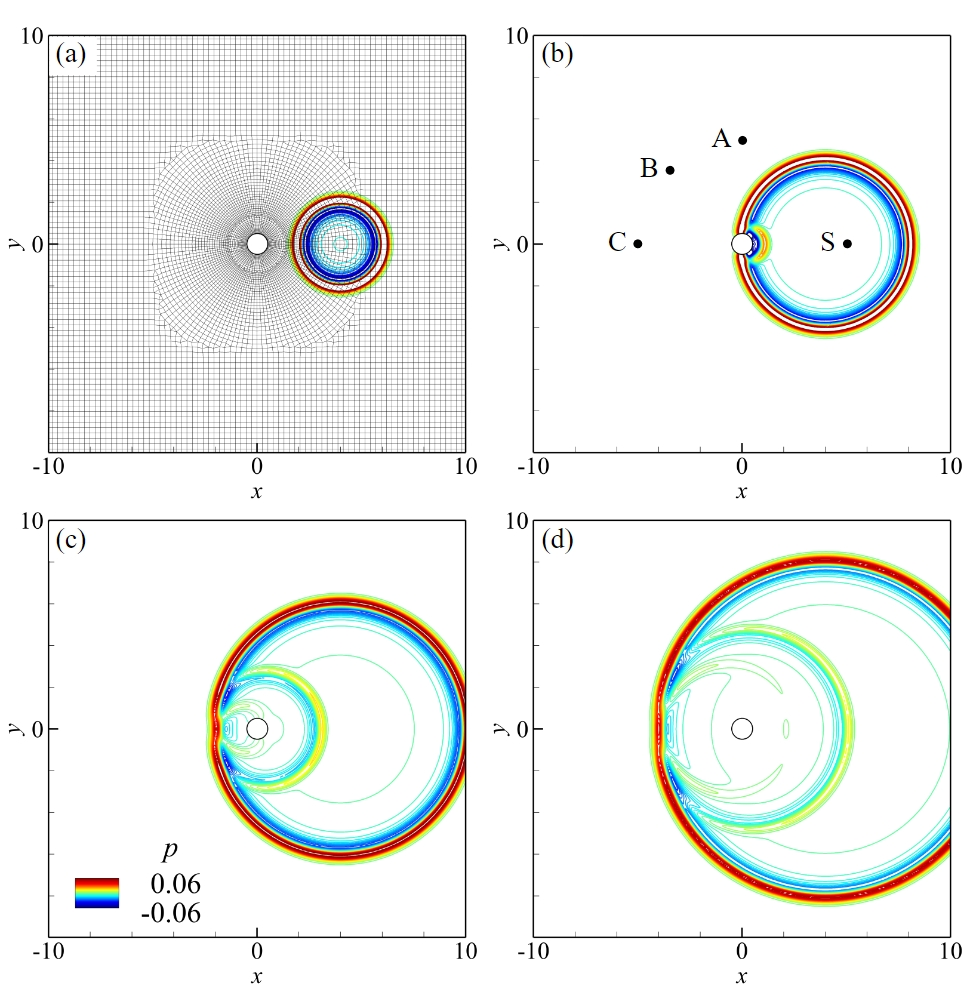
图 2 基于高阶通量重构方法求解高斯脉冲圆柱散射